Problem Description
Relativistic Travel Calculator RTC7681 is a software intended to calculate various variables and graph various function over time related to relativistic travel. The variables used in this blog entry are :
| - | MShip | : | The rest empty mass of the spaceship intended to be used. |
| - | MFuel | : | The rest mass of the fuel provided for the spaceship. |
| - | FBT | : | Amount (mass) of fuel burned per unit time. |
| - | EPM | : | The amount of energy provided per unit mass of fuel burned. |
| - | DistanceOfDestination | : | The distance between spaceship's destination and its origin. |
The calculation done in RTC7681, assumes that :
- The spaceship travel in linear trajectory.
- The spaceship always use the same engine capacity for both acceleration and deceleration.
- Friction with interstellar medium is ignored.
- The total rest mass of the spaceship is decreasing as the spaceship engine burn the fuel.
Below are the definition of several terms used in this blog entry :
| - | IRF | : | Inertial Reference Frame, any IRF values are measured by observers in the origin. |
| - | SRF | : | Ship's Reference Frame, any IRF values are measured by observers inside the ship. |
| - | Acceleration Time | : | The time required by the spaceship to accelerate to an intended maximum IRF velocity. |
| - | Acceleration Distance | : | Distance travelled by the ship during Acceleration Time. |
| - | Deceleration Time | : | The time required by the spaceship to decelerate to zero IRF velocity. |
| - | Deceleration Distance | : | Distance travelled by the ship during Deceleration Time. |
Function of Velocity, Time, Distance and Acceleration
In order to find the function that relate these variables, we have to remember a concept called energy preservation. To gain kinetic energy, something have to lose its potential energy. The potential energy of the ship is stored as mass of fuel, while the kinetic energy of the ship as a whole depend on the total mass of the ship and fuel, multiplied by the square of its velocity, dilated by the mass dilation caused by relativistic velocity. From the equivalence between ship's potential and kinetic energy, we got we got :
Equation RTC7681-0. Energy Preservation
Equation RTC7681-1. Energy Preservation
To Solve this for v and t, we have to do the following steps :
Equation RTC7681-2. Energy Preservation
Equation RTC7681-3. Energy Preservation
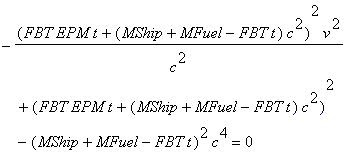
Equation RTC7681-4. Quadratic Equation relative to v
Since equation RTC7681-4 is a Quadratic Equation relative to v, we can use any technique used to solve a Quadratic Equation , to solve it for v. Assuming that v is positive, we got the function of v over t below :
Equation RTC7681-5. Function of velocity over time
function TForm1.CalculateVelo(const EPMA,FBTA,MS,MF,t : double ) : double; var P1,P2,PL,t2,FBT2,EPM2 : double; begin FBT2:=FBTA*FBTA; EPM2:=EPMA*EPMA; t2:=t*t; PL:=((2*EPMA*FBTA*t*c2*(MF+MS))-(2*FBT2*EPMA*t2*c2)+(FBT2*EPM2*t2)); P1:=sqrt(abs(PL)); P2:=c2*(MF+MS)+FBTA*(EPMA-c2)*t; CalculateVelo:=P1*c/P2; end; |
Equation RTC7681-5 in Delphi Code
By turning equation RTC7681-4 to it's alternative form below, we can easily see that equation RTC7681-4 is a Quadratic Equation relative to t.
Equation RTC7681-4B. Quadratic Equation relative to t
So assuming that t is positive, we got the function of t over v below :
Equation RTC7681-6. Function of time over velocity
function TForm1.CalculateTime(const EPMA,FBTA,MS,MF,v : double ) : double; var P1,P2,P3,v2,EPM2 : double; begin v2:=v*v; EPM2:=EPMA*EPMA; P2:=c2*EPM2*(c2-v2); P1:=EPMA*(c2-v2)+v2*c2-sqrt(P2); P2:=c2*(MS+MF); P3:=((v2*EPM2)+(v2*c2*c2)-(c2*EPM2)+(2*c2*c2*EPMA)-(2*v2*EPMA*c2))*FBT; CalculateTime:=P1*P2/P3; end; |
Equation RTC7681-6 in Delphi Code
Acceleration and Deceleration Distance over time can be calculated using numerical integration below of the equation below :
Equation RTC7681-7. Function of Acceleration Distance over Time
function Torm1.CalculateDist(const EPMA,FBTA,MS,MF,t0,t1 : double ) : double; var Acc,DT,Y0,Y1,lt : double; hi : cardinal; begin DT:=(t1-t0)/400; lt:=t0; Y0:=CalculateVelo(EPMA,FBTA,MS,MF,t0); Acc:=0; for hi:=1 to 400 do begin lt:=lt+DT; Y1:=CalculateVelo(EPMA,FBTA,MS,MF,lt); Acc:=Acc+0.5*(Y1+Y0); Y0:=Y1; end; Acc:=Acc*DT; CalculateDist:=Acc; end; |
Equation RTC7681-7 in Delphi Code
While the amount of acceleration and deceleration over time is the differentiation result of v over t.
Equation RTC7681-8. Function of Acceleration over time
Maximum Amount of Fuel Expended during Acceleration Time
The amount of fuel expended during acceleration time should never exceed a certain value or the ship will not be have enough fuel later during deceleration time. The maximum mass of fuel expendeable during acceleration will be called MPF here on. To find the value of MPF, remember that the proportion between the amount of fuel required to accelerate an object and the mass of the object, is always the same for the same velocity. Which means :
So, if the spaceship is intended to stop in its destination, the amount of fuel expended during acceleration should never be greater than MPF.
Exception in Acceleration Distance
Sometimes after some calculation, amount of fuel required to be expended during both acceleration and deceleration phase are not as great as we first intended them to be. In such situation, the amount of fuel required to be expended must be recalculated. The recalculation will involve solving equation RTC7681-9 for t0 and t1 :
Equation RTC7681-9. Exception Handling Formula
The variables in the equations above are :
| - t0 | : | Length of Acceleration Phase. |
| - t1 | : | Length of Deceleration Phase. |
| - MFuel0 | : | Initial amount of fuel when the spaceship start accelerating. |
| - MFuel1 | : | Initial amount of fuel when the spaceship start decelerating. |
We also have to mind the fact that the Initial amount of fuel when the spaceship start decelerating is equal with the Initial amount of fuel when the spaceship start accelerating subtracted with the amount of fuel burned during Acceleration Phase.
MFuel1 = MFuel0 - FBT t0
No comments:
Post a Comment