An Example of Orphys Fractal

It is suggested to read Introduction to Orphys Production Line and Shipping Schedule Optimation, before reading this entry.

Heuristic Constants in Optimation Program

The effectiveness of the optimation algorithm used in Orphys Production Line and Shipping Schedule Optimation (OPLSSO) , is affected by a set of heuristics. These measure of effectiveness, is often called fitness in Genetic Algorithm terms. By plotting the value of several objective functions into a two dimensional map, given a set of heuristic values, it is possible to compare the effectiveness of each set of heuristics.

As the number of heuristic values in Orphys PLSSO is more than two, the actual map is multidimensional. Since the computation resources I have is limited, I can only plot some two dimensional manifold inside the multidimensional map. The mathematic detail of what is plotted is given below.

For example an optimation algorithm have a set of objective values : Z₁, Z₂, Z₃, ...... , Z_k
The values of these objective values depend on a set of heuristics : h₁, h₂, h₃, ...... , h_n
A function F, will map a set of heuristics to the set of objective values as follow : [ Z_1..k ] = F( h_1..n );

Where k is the number of objective values and n is the number of heuristics used.

Since we have to plot a two dimensional map with two axis x and y, we have to make the value of the set of heuristics to depend on the value of x and y in linear manner :
h₁ = a₁ x + b₁ y + c₁
h₂ = a₂ x + b₂ y + c₂
h₃ = a₃ x + b₃ y + c₃
.
.
.
h_n = a_n x + b_n y + c_n

Now the function F will map the value of x and y to the value of [ Z_1..n ], like below :
[ Z_1..k ] = F( a_1..n x + b_1..n y + c_1..n );

The Objective Values of Orphys Production Line and Shipping Schedule Optimation

In case of Orphys PLSSO, the set of objective values are :

1. Total Production Line Time Used

How many Production Line Hour are used if a set of heuristics is used to control the algorithm used in Orphys PLSSO, according to the schedule produced by a set of heuristics ?

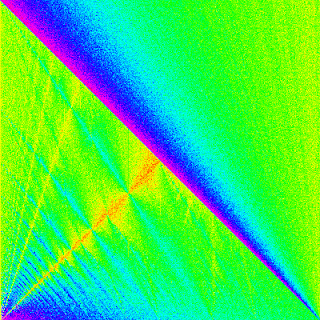
The coloring used in the map below is HSV, with red denoting an area where the sets of heuristics produce a schedule with lowest amount of Production Line Hour used, and purple denoting an area where the sets of heuristics produce a schedule with highest amount of Production Line Hour Used. The less Total Production Line Hour used, the more favourable the schedule produced is.

2. Total Overtime Hour Used

How many hours must the Production Lines in the case must works outside normal workhour, so customer's demand can be fulfilled on time, according to the schedule produced by a set of heuristics ?

The coloring used in the map below is HSV, with red denoting an area where the sets of heuristics produce a schedule with lowest amount of Total Overtime Hour Used, and purple denoting an area where the sets of heuristics produce a schedule with highest amount of Total Overtime Hour Used. The less Total Overtime Hour used, the more favourable the schedule produced is.

3. Total Production Line Salary

How much money must be spended to pay the salary, according to the schedule produced by a set of heuristics ? This value include the normal workhour salary and overtime payment.

The coloring used in the map below is HSV, with red denoting an area where the sets of heuristics produce a schedule with lowest Total Production Line Salary, and purple denoting an area where the sets of heuristics produce a schedule with highest Total Production Line Salary. The less Total Production Line Salary is required, the more favourable the schedule produced is.

4. Total Inter-Warehouse Shipping Cost

How much money must be spended to move the products from factories to warehouses or between warehouses, according to the schedule produced by a set of heuristics ?

The coloring used in the map below is HSV, with red denoting an area where the sets of heuristics produce a schedule with lowest Total Inter-Warehouse Shipping Cost, and purple denoting an area where the sets of heuristics produce a schedule with highest Total Inter-Warehouse Shipping Cost. The less Total Inter-Warehouse Shipping Cost is required, the more favourable the schedule produced is.

5. Total To-Customer Shipping Cost

How much money must be spended to send finished products from company's warehouses to customers on time, according to the schedule produced by a set of heuristics ? This value is affected by the amount of time left ( relative to deadline ) when the products that customers ordered is finished, the cost of the shipping means required to deliver the products on time, and the amount of products delivered.

The coloring used in the map below is HSV, with red denoting an area where the sets of heuristics produce a schedule with lowest Total To-Customer Shipping Cost, and purple denoting an area where the sets of heuristics produce a schedule with highest Total To-Customer Shipping Cost. The less Total To-Customer Shipping Cost is required, the more favourable the schedule produced is.

6. Order Fulfillment Cost Grand Total

Order Fulfillment Cost Grand Total is the predicted sum of all money used in all activity required to fulfill customer's demand. This cost is the sum of production line salary, inter-warehouse shipping cost, and to-customer shipping cost. So this value is the ultimate objective value of Orphys PLSSO.

The coloring used in the map below is HSV, with red denoting an area where the sets of heuristics produce a schedule with lowest Order Fulfillment Cost Grand Total, and purple denoting an area where the sets of heuristics produce a schedule with highest Order Fulfillment Cost Grand Total. The less Order Fulfillment Cost Grand Total is required, the more favourable the schedule produced is.

By comparing the maps of different objective values to Order Fulfillment Cost Grand Total map, we can understand which cost is dominant in a company. By understanding which cost is dominant in a company, the management team of a company can reduce the total cost by focusing on how to reduce the dominant cost. For example, since the map for Order Fulfillment Cost Grand Total is roughly the same with Total To-Customer Shipping Cost map ( in this example ) , we can infer that To-Customer Shipping Cost is the dominant one, and company's management team can focus their cost cutting efforts, by finding new means for shipping their finished products to customer.

Download an Example of Orphys PLSSO Schedule. ( HTML )